Movimiento de un campo magnetico

Una partícula que se mueve en un campo magnético experimenta una fuerza dada por el producto vectorial Fm=q·vxB. El resultado de un producto vectorial es un vector de

módulo igual al producto de los módulos por el seno del ángulo comprendido qvB senq

dirección perpendicular al plano formado por los vectores velocidad v y campo B.

y el sentido se obtiene por la denominada regla del sacacorchos. Si la carga es positiva el sentido es el del producto vectorial vxB, como en la figura izquierda

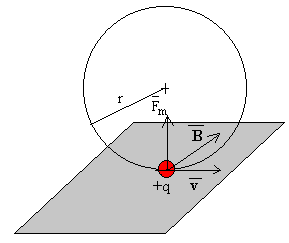
Si la carga es negativa el sentido de la fuerza es contrario al del producto vectorial vxB

Elementos a destacar de esta fórmula es que la fuerza magnética se deja notar, por tanto, sólo sobre partículas cargadas; para partículas neutras () se tendrá que . Un hecho aún más reseñable es que sólo actúa sobre partículas en movimiento. Si una partícula está en reposo respecto a nuestro sistema de referencia la fuerza magnética ejercida sobre ella, aunque esté cargada y exista un campo magnético, es nula.

La unidad de campo magnético en el Sistema Internacional es el Tesla.  Dimensionalmente un Tesla será 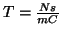    Newton segundo entre metro Culombio.



La fuerza magnética siempre es perpendicular a la trayectoria de la partícula. Por tanto el trabajo efectuado por la fuerza magnética es siempre cero y la energía cinética se conserva.

Si, además de un campo magnético existiera un campo eléctrico  podemos incluir esta fuerza en la Ley de Lorentz y, como la fuerza eléctrica es simplemente  y podemos usar el principio de superposición